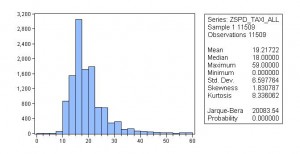
对于滑行时间我还学着做了一个实验，实验内容是夏季和冬季的滑行时间是否相同？因为上海的天气夏季吹东南风，冬季吹西北风。跑道都是南北向的，由于从停机位滑行至两个跑道头的距离不同，因此我觉得滑行时间应该是不相同的。让我们用数据来检验这个假设：

首先我用和实验1相同的方法计算出了以下数据：

设定一个零假设：夏季的滑行时间和冬季的滑行时间相同，所以有 夏季均值- 冬季均值 = 0。
设定一个备用假设： 夏季的滑行时间和冬季的滑行时间不相同，所以有 夏季均值 – 冬季均值 不等于 0。

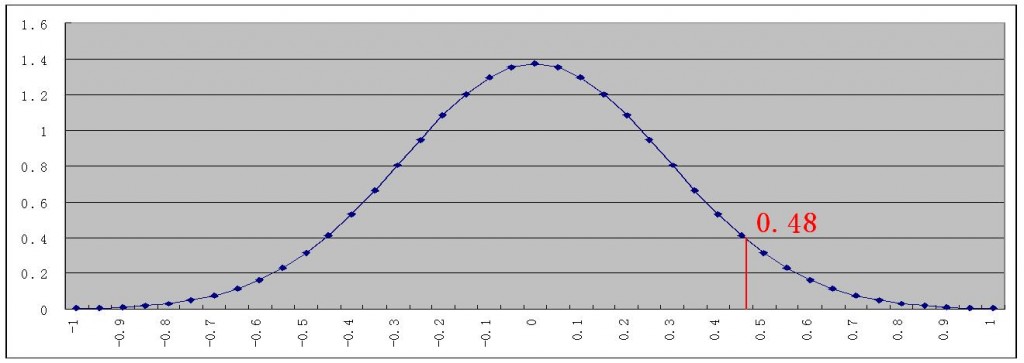
在5%的显著性水平下，界限值为1.65个标准差，也就是 0.29069 × 1.65 = 0.479648。用零假设，也就是“夏季均值- 冬季均值 = 0”，也就是“均值为0”做一个样本之差的正态分布如下图：

再用数据中样本之差1.89104和0.48做对比，可以发现，1.89明显在界限值0.48之外。因此可以拒绝零假设，接受备用假设。

结论，在5%的显著性水平下，我可以说夏季的滑行时间和冬季的滑行时间明显不同。因此，在设定飞行计划的滑行时间时，应该把夏季和冬季的滑行时间分开设定。

我一直对统计学有着浓厚的兴趣，可惜大学时的知识都荒废了。最近在带孩子之余看了点网易公开课的统计学入门，受益匪浅。一下内容就当是一次实验。如有错误之处，望指出。

首先，我从数据库中导出了最近一年所有737NG飞机的浦东机场出港撤轮档时间和实际起飞时间，两者之差就是滑行时间。选择737机型是因为737的ACARS比老飞机好。推出时间准确，减少手工输入时间上的偏差。不过还是有3%左右的数据是不符合逻辑的，可以从数据中剔除。最后有效数据一共11509个。

以下是这11509个数据的分布图，均值19.21772分钟，标准差6.597764分钟：

从偏度和峰度看都不能看作正态分布。根据中心极限定理，N次抽样后，抽样的均值就会服从正态分布。抽样的个数我选择11509/365=31.53，也就是平均每一天浦东的出港航班数。以下是抽样的均值分布图，均值19.22，标准差1.1749：

如果要求99.9%的置信区间，查表得3.1个标准差。19.22 + 1.1749 × 3 = 22.86分钟。

结论：我可以有99.9%的信心保证，过去一年中的任何一天，在浦东出港的滑行时间的平均值都在22.86分钟以下。